


Next: Analysis of Significant Genotypes
Up: Detailed Analysis of a
Previous: Flaw Period and Proportion
Activity Measures
The activity wave plots for the standard run and its neutral shadow
are shown in Figures 5.13 and 5.14
respectively. These two figures are plotted to the same scale. A
magnified version of the neutral shadow plot in shown in
Figure 5.15.
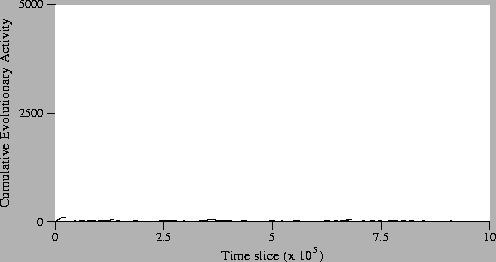
The first point to note is that in the neutral shadow, compared to the
standard run, there are no significant waves at all. In other
words, no individual genotypes achieved significant continued adaptive
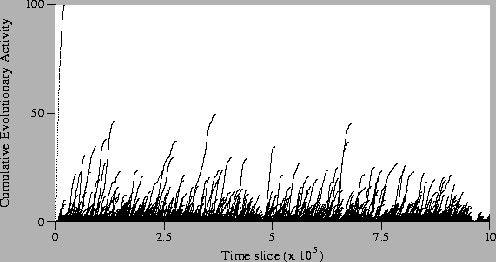
success in this run. Even if we look at the magnified plot of the
neutral shadow (Figure 5.15), we see that the
pattern of activity is very different to the standard run
(Figure 5.13). In the neutral shadow, there are many
more activity waves than in the standard run, but they generally
survive for a much shorter duration. These observations were expected
(because operations are executed on randomly-chosen individuals in the
neutral shadow), and they suggest that the significant activity
observed in the standard run (Figure 5.13) is
due to the adaptive success of the individual genotypes concerned.
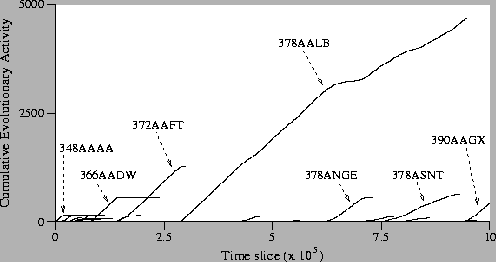
Figure:
Standard Run: Activity Waves Plot.
|
Figure:
Standard Run, Neutral Shadow: Activity Waves Plot.
|
Figure:
Standard Run, Neutral
Shadow: Activity Waves Plot (magnified).
 |
Looking at the activity waves of the standard run, we see that the
ancestor genotype (348AAAA) is fairly quickly replaced by other
genotypes. The first variant to enjoy notable continued adaptive
success is genotype 366AADW, which first appears at time 76,100. At
time 130,100 a new genotype, 372AAFT, appears, and gradually
outcompetes 366AADW. By time 146,400 only a single program of genotype
366AADW remains, although this program manages, somewhat impressively,
to survive for a further 91,700 time slices, living right up
to time 238,100. At time 274,700, genotype 378AALB appears on the
scene. This genotype quickly displaces 372AAFT, and remains the
dominant genotype in the population right up until time 955,100, under
5000 time slices short of the end of the run. During its long reign,
378AALB is challenged a small number of times, most notably by the
variants 378ANGE and 378ASNT. These variants are both of length equal
to the dominant genotype, and both eventually lose their challenge
and are driven to extinction. Having seen off these challenges,
genotype 378AALB remained the dominant type of program for a short
while longer. However, at time 925,700 a new genotype, 390AAGX, is
born. Within 25,000 time slices, it drives 378AALB to extinction, and
at the end of the run 390AAGX is the final dominant genotype.
The graphs of Cumulative Activity, Mean Cumulative Activity, New
Activity and Mean New Activity, for the standard run and its neutral
shadow, are shown in
Figures 5.16-5.23.
Looking at the graph of Cumulative Activity in the standard run
(Figure 5.16), we can see that it reflects the shape
of the activity wave plot (Figure 5.13). This is
because the value plotted in Figure 5.16 is the sum of
the activities of all the individual genotypes at a given point in the
run (i.e. the sum of all the waves present at any given moment in
Figure 5.13). As a single wave tends to dominate the
activity wave plot at most points during the run, the activity value
of that genotype largely determines the shape of
Figure 5.16. The diversity of genotypes in the
standard run is usually very low (Figure 5.5), so
the graph of Mean Cumulative Activity (defined at any given time as
Cumulative Activity divided by Diversity), also has a similar shape
(Figure 5.18).
The graphs of Cumulative Activity and Mean Cumulative Activity for the
neutral shadow (Figures 5.17 and
5.19) show again (as we saw in the activity wave
plot of Figure 5.14) that there was no significant
cumulative evolutionary activity in the neutral shadow compared to the
standard run.
Figure:
Standard Run: Cumulative
Activity.
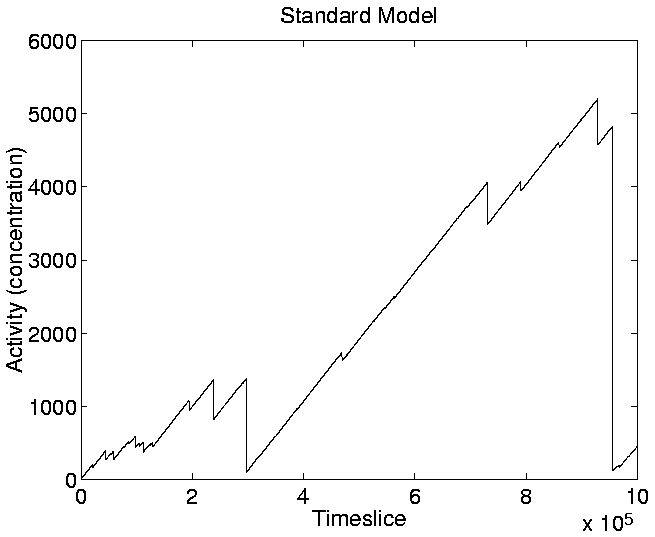
|
Figure:
Standard Run, Neutral
Shadow: Cumulative Activity.
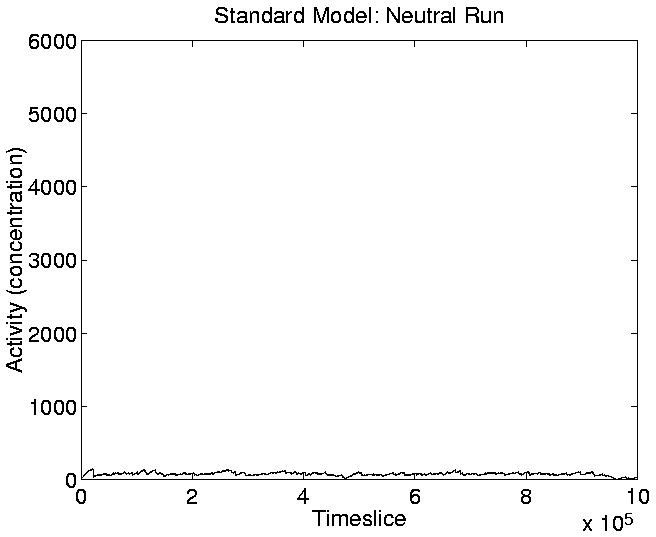
|
Figure:
Standard Run: Mean
Cumulative Activity.
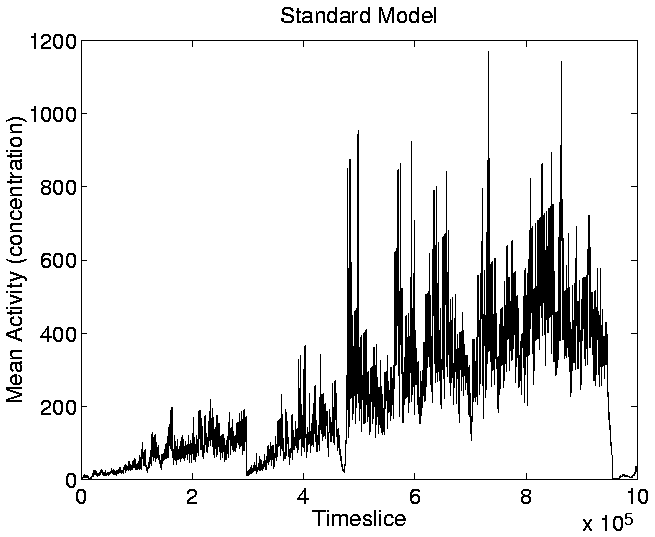
|
Figure:
Standard Run, Neutral Shadow: Mean Cumulative Activity.
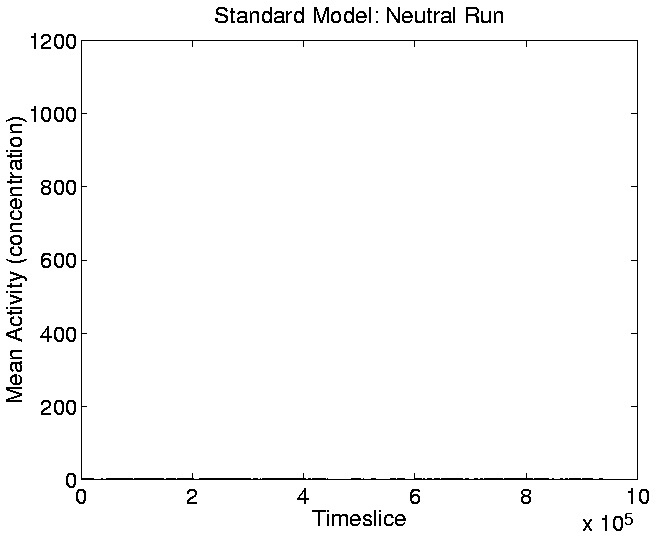
|
The graphs for New Activity, reflecting the introduction of new
genotypes with adaptive significance, are shown in
Figures 5.20-5.23. The
parameter a0, which determines the lowest level of activity that
is taken to indicate adaptive significance, was set at the lowest
level such that the neutral shadow produced zero new activity
throughout the run. The value chosen for a0 was 150, and for the
upper activity limit, a1, the value chosen (somewhat more
arbitrarily) was 300. When applying the same thresholds to the
standard run (Figures 5.20 and
5.22), we can see that this measure clearly
indicates the points during the run at which significant new genotypes
were introduced (c.f. Figure 5.13).
In [Bedau et al. 98], a scheme is presented for classifying
evolutionary systems into (at least) three distinct classes, depending
on whether adaptive evolutionary activity is absent (class 1), bounded
(class 2), or unbounded (class 3). The classification of a system is
determined by its diversity D, mean cumulative activity
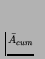 ,
and mean new activity
,
and mean new activity
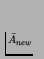 .5.9 If
the system has bounded D, zero
.5.9 If
the system has bounded D, zero
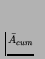 and zero
and zero
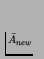 ,
it belongs to class 1 (no adaptive evolutionary
activity). If it has bounded5.10 D,
bounded
,
it belongs to class 1 (no adaptive evolutionary
activity). If it has bounded5.10 D,
bounded
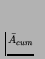 and positive5.11
and positive5.11
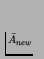 ,
it
belongs to class 2 (bounded adaptive evolutionary activity). If it has
unbounded D, bounded
,
it
belongs to class 2 (bounded adaptive evolutionary activity). If it has
unbounded D, bounded
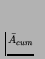 and positive
and positive
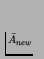 ,
it
belongs to class 3 (unbounded adaptive evolutionary activity).
Bedau and colleagues claim that the biosphere (at least with
consideration to the Phanerozoic fossil record), belongs to class 3,
whereas all artificial evolutionary systems they have studied belong
to classes 1 and 2. From this perspective, a major challenge for the
field of artificial life is to produce an artificial evolutionary
system which exhibits class 3 dynamics.
,
it
belongs to class 3 (unbounded adaptive evolutionary activity).
Bedau and colleagues claim that the biosphere (at least with
consideration to the Phanerozoic fossil record), belongs to class 3,
whereas all artificial evolutionary systems they have studied belong
to classes 1 and 2. From this perspective, a major challenge for the
field of artificial life is to produce an artificial evolutionary
system which exhibits class 3 dynamics.
This classification scheme is not perfect, as we can never be sure
whether the results of a limited run of a system (which might have led
us to suppose, for example, that D is bounded) will hold true for a
much longer run (e.g. D might actually turn out to be unbounded).
However, it is at least a step in the right direction,
towards a rigorous classification of evolutionary dynamics. According
to the scheme, and based upon the results reported in this section,
Cosmos would be classified as class 2--the same as various other
artificial evolutionary systems. Despite its weaknesses, the
scheme does at least indicate that the type of evolution evidenced by
the fossil record may be qualitatively different to that observed in
our artificial systems.
Figure:
Standard Run: New Activity.
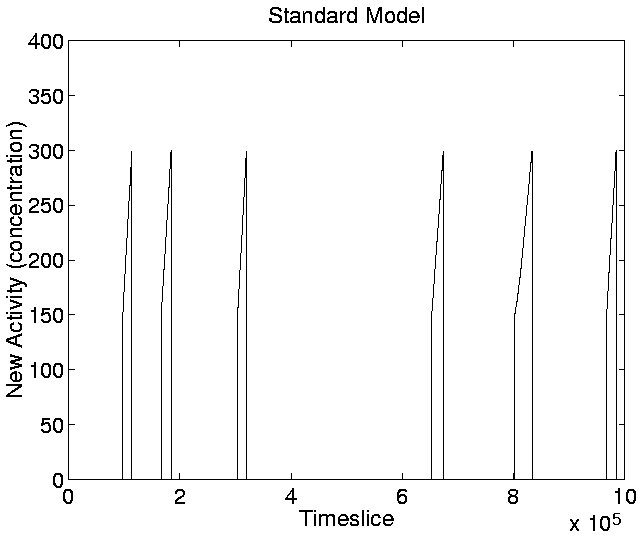
|
Figure:
Standard Run, Neutral Shadow: New Activity.
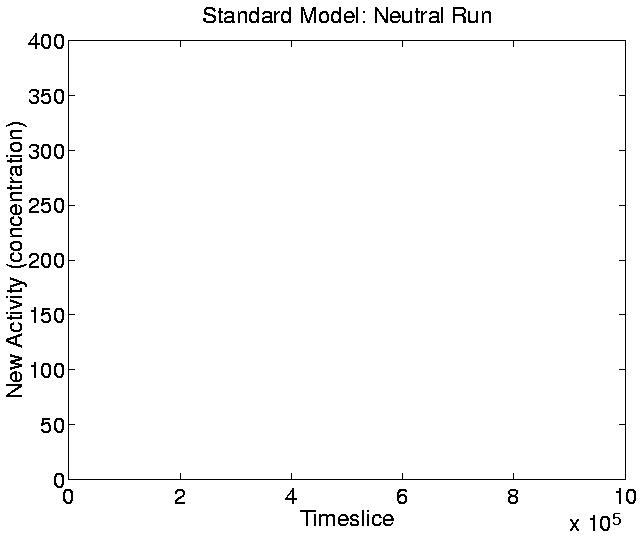
|
Figure:
Standard Run: Mean New Activity.
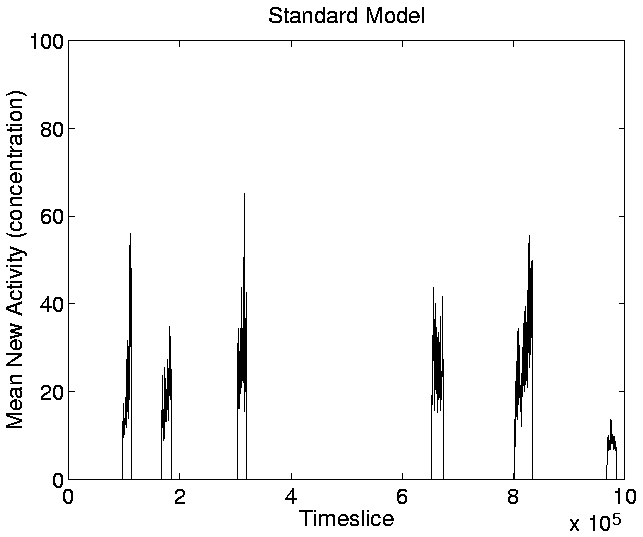
|
Figure:
Standard Run, Neutral Shadow: Mean New Activity.
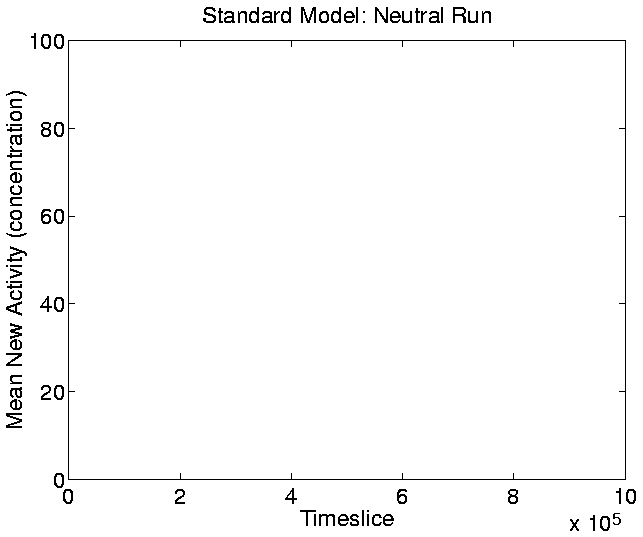
|



Next: Analysis of Significant Genotypes
Up: Detailed Analysis of a
Previous: Flaw Period and Proportion
Tim Taylor
1999-05-29










![]() ,
and mean new activity
,
and mean new activity
![]() .5.9 If
the system has bounded D, zero
.5.9 If
the system has bounded D, zero
![]() and zero
and zero
![]() ,
it belongs to class 1 (no adaptive evolutionary
activity). If it has bounded5.10 D,
bounded
,
it belongs to class 1 (no adaptive evolutionary
activity). If it has bounded5.10 D,
bounded
![]() and positive5.11
and positive5.11
![]() ,
it
belongs to class 2 (bounded adaptive evolutionary activity). If it has
unbounded D, bounded
,
it
belongs to class 2 (bounded adaptive evolutionary activity). If it has
unbounded D, bounded
![]() and positive
and positive
![]() ,
it
belongs to class 3 (unbounded adaptive evolutionary activity).
Bedau and colleagues claim that the biosphere (at least with
consideration to the Phanerozoic fossil record), belongs to class 3,
whereas all artificial evolutionary systems they have studied belong
to classes 1 and 2. From this perspective, a major challenge for the
field of artificial life is to produce an artificial evolutionary
system which exhibits class 3 dynamics.
,
it
belongs to class 3 (unbounded adaptive evolutionary activity).
Bedau and colleagues claim that the biosphere (at least with
consideration to the Phanerozoic fossil record), belongs to class 3,
whereas all artificial evolutionary systems they have studied belong
to classes 1 and 2. From this perspective, a major challenge for the
field of artificial life is to produce an artificial evolutionary
system which exhibits class 3 dynamics.



