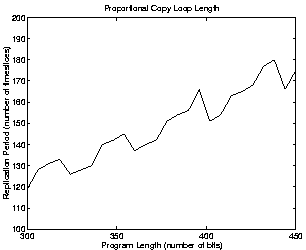


Next: Replication Period
Up: Detailed Analysis of a
Previous: Detailed Analysis of a
Program Length
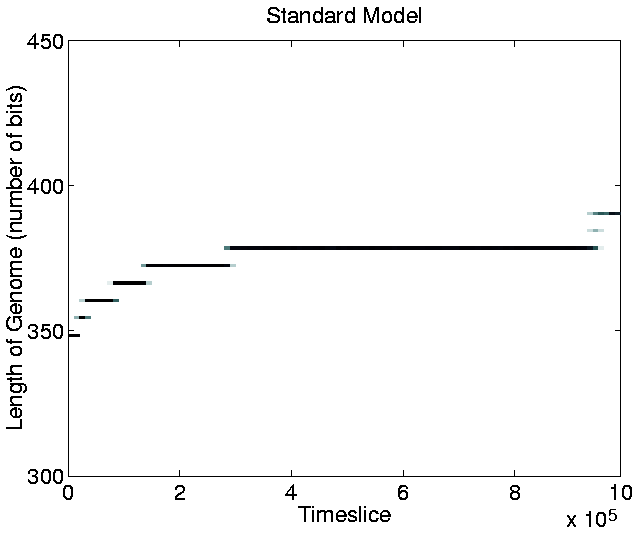
The change in program length over the run is shown in
Figure 5.2. A number of interesting points are
apparent from this graph. The most obvious one is that there is a
trend for increasing program length over the course of the run. The
length of the ancestor programs was 348 bits, but by the end of the
run, virtually all of the programs in the population were of length 390
bits.5.7
Recalling from the previous chapter that each instruction is
represented by 6 bits, this increase in length corresponds to an extra
7 instructions being added to the ancestor.
Figure:
Standard Run: Length.
|
Figure:
Standard Run: Population Size.
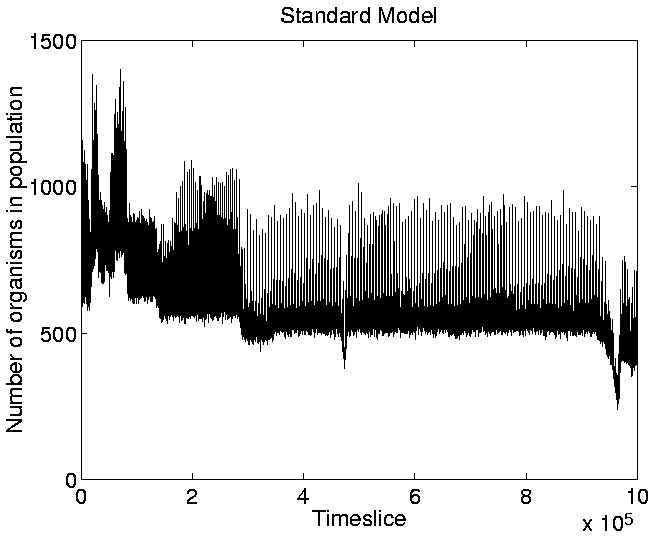
|
Figure:
Standard Run: Replication Period.
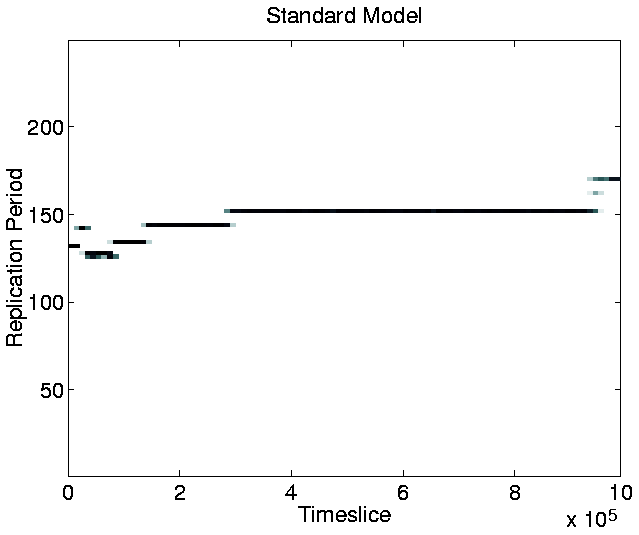
|
Figure:
Standard Run: Diversity.
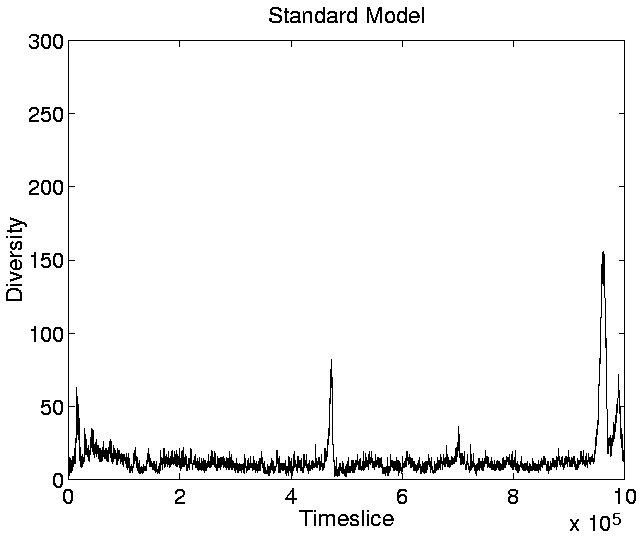
|
Figure:
Standard Run: Flaw Period.
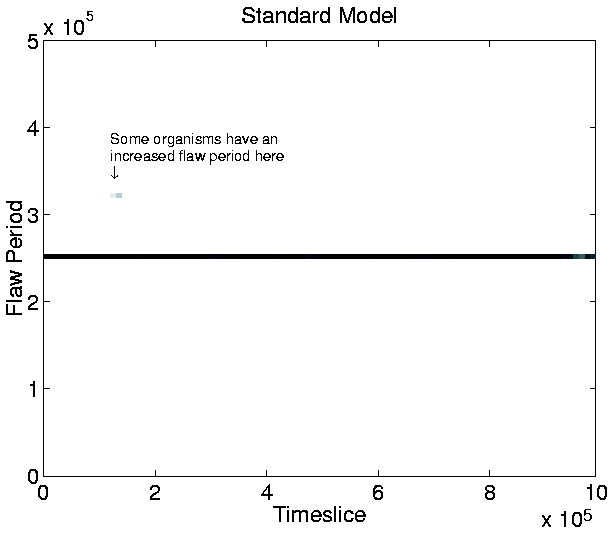 |
Figure:
Standard Run: Age at Death.
 |
Another point of interest in the graph is that, at any given time
during the run, the population tends to be composed of organisms of
only a single length.5.8 The only exception to this occurs during a
transition phase from programs of one length to programs of a greater
length. During these phases, progams of two, or, occasionally, three
different lengths coexist, but the shorter programs soon die out, to
be completely replaced by the longer ones.
This result is in contrast to those of similar runs on Tierra, where
shorter ``parasite'' programs evolved and coexisted with the longer
programs (as described in Section 3.2.1). As discussed in
Section 3.3.1, the non-appearance of parasites was
expected, because Cosmos does not allow cells to execute the code of
other cells.
The increase in program length, on the other hand, was unexpected.
During each timeslice, CPU-time was allocated to each program (if it
had enough energy) according to its length, so that, all else being
equal, selection was size neutral (see
Section 4.2.3). However, the picture is
complicated by the fact that the program has to cycle once round the
``copy loop'' to copy each instruction. In the ancestor, the copy loop
accounts for 19 of the 58 instructions, or approximately one third of
the total number. The total number of instructions, I, that must be
executed to replicate the program is therefore approximately:
where
 is the number of instructions not involved in the
copy loop (58-19=39), Nloop is the number of instructions in
the copy loop (=19), and Ntotal is the total number of
instructions (=58). In this case, I is therefore
39+19*58=1141 instructions. (This is not exactly right,
because there are some conditional instructions, and the templates at
the beginning and end of the program do not actually get executed, but
it is near enough.) Now, during this run, the parameter
et_value_constant was set to 0.025, so at each timeslice
the ancestor (of length 58 instructions, or 58*6=348 bits) was
allowed to run
is the number of instructions not involved in the
copy loop (58-19=39), Nloop is the number of instructions in
the copy loop (=19), and Ntotal is the total number of
instructions (=58). In this case, I is therefore
39+19*58=1141 instructions. (This is not exactly right,
because there are some conditional instructions, and the templates at
the beginning and end of the program do not actually get executed, but
it is near enough.) Now, during this run, the parameter
et_value_constant was set to 0.025, so at each timeslice
the ancestor (of length 58 instructions, or 58*6=348 bits) was
allowed to run
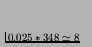 instructions (rounded down to a whole
number). The total number of timeslices required for an ancestor
program to replicate itself is therefore approximately
instructions (rounded down to a whole
number). The total number of timeslices required for an ancestor
program to replicate itself is therefore approximately
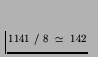 timeslices.
timeslices.
Similar calculations can be made for programs of different lengths. If
we assume that the size of the copy loop is always one third of the
size of the whole program, the results we get are as shown in the
left-hand side of Figure 5.8. In this case,
longer programs still take longer to replicate, so we would still
expect selection for shorter programs. (The graph looks somewhat
erratic because of the effects of rounding down the number of
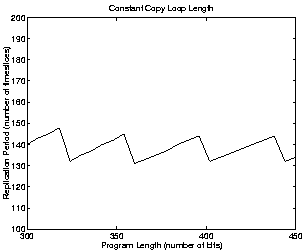
instructions per time slice to an integer value, etc.) If however we
assume that the size of the copy loop is constant no matter how long
the program, the results are somewhat different (see the right-hand
side of Figure 5.8). In this case, the
assumption of length-neutral selection is more realistic.
As an increase in program length was observed, we might therefore
expect the extra instructions to have been added outside of the copy
loop.
However, as the allocation of CPU-time is also dependent on a program
having enough stored energy, it is possible that the observed increase
in program length might be associated with the evolution of programs
that collect and store more energy from the environment. In this case,
it might even benefit programs to add more energy collection
instructions inside the copy loop, as each one will then be executed
during every iteration of the loop.
The true cause of the increase in program length will be investigated
in Section 5.2.7.
Figure:
Theoretical
Relationship between Program Length and Replication Period. Left:
Size of copy loop increases proportionally with size of
program. Right: Size of copy loop is constant.
|
|



Next: Replication Period
Up: Detailed Analysis of a
Previous: Detailed Analysis of a
Tim Taylor
1999-05-29












 is the number of instructions not involved in the
copy loop (58-19=39), Nloop is the number of instructions in
the copy loop (=19), and Ntotal is the total number of
instructions (=58). In this case, I is therefore
39+19*58=1141 instructions. (This is not exactly right,
because there are some conditional instructions, and the templates at
the beginning and end of the program do not actually get executed, but
it is near enough.) Now, during this run, the parameter
et_value_constant was set to 0.025, so at each timeslice
the ancestor (of length 58 instructions, or 58*6=348 bits) was
allowed to run
is the number of instructions not involved in the
copy loop (58-19=39), Nloop is the number of instructions in
the copy loop (=19), and Ntotal is the total number of
instructions (=58). In this case, I is therefore
39+19*58=1141 instructions. (This is not exactly right,
because there are some conditional instructions, and the templates at
the beginning and end of the program do not actually get executed, but
it is near enough.) Now, during this run, the parameter
et_value_constant was set to 0.025, so at each timeslice
the ancestor (of length 58 instructions, or 58*6=348 bits) was
allowed to run
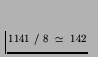 timeslices.
timeslices.